შემოკლებული გამრავლების ფორმულები
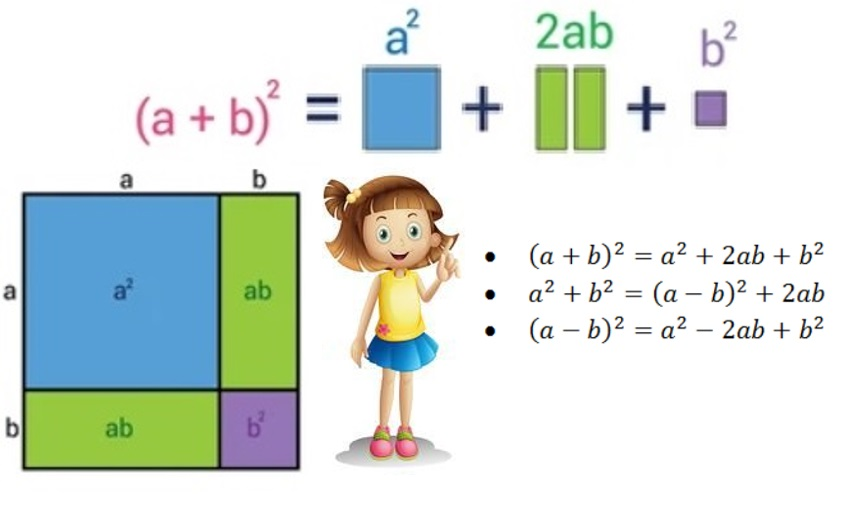
0
ეს არის საკითხი მათემატიკაში, რომელიც ერთ დროს ძალიან მიყვარდა. ერთი შეხედვით ძალიან მარტივია, ამავდროულად ღრმა და მეტად საინტერესო, ფაქტებს რომელსაც აქ მოვიყვანთ მეტად საინტერესოს გახდის ამ ფორმულებს. გავხადოთ მათემატიკა უფრო საინტერესო! მაშ ასე:
1. ჯამის და სხვაობის კვადრატის გამოსათვლელი ფორმულები:
(a + b)2=a2 + 2ab + b2 ორი გამოსახულების ჯამის კვადრატი ტოლია პირველი გამოსახულების კვადრატს დამატებული გაორკეცებული ნამრავლი პირველი გამოსახულებისა მეორეზე და დამატებული მეორე გამოსახულების კვადრატი.
(a - b)2=a2 - 2ab + b2 ორი გამოსახულების სხვაობის კვადრატი ტოლია პირველი გამოსახულების კვადრატს გამოლებული გაორკეცებული ნამრავლი პირველი გამოსახულებისა მეორეზე და დამატებული მეორე გამოსახულების კვადრატი.
არა მხოლოდ ორი რიცხვის ჯამი იშლება, არამედ ნებისმიერი რაოდენობის შესაკრები:
(a + b + c)2=a2 + b2 + c2 + 2ab + 2ac + 2bc
2. კვადრატების ჯამისა და სხვაობის გამოსათვლელი ფორმულები:
a2 - b2=(a - b)(a + b) ორი გამოსახულების ჯამის ნამრავლი მათსავე სხვაობაზე ტოლია მათივე კვადრატების სხვაობის.
a2 + b2=[არ იშლება R-ში (ნამდვილ რიცხვებში), თუმცა C-ში (კომპლექსურ რიცხვთა სიმრავლეში) a2 + b2=(a+bi)(a-bi), სადაც i2=-1]
3.ჯამის და სხვაობის კუბის ფორმულები:
(a + b)3=a3 + 3a2b + 3ab2 + b3 ორი გამოსახულების ჯამის კუბი ტოლია პირველი გამოსახულების კუბს დამატებული გასამკეცებული ნამრავლი პირველი გამოსახულების კვადრატისა მეორეზე დამატებული გასამკეცებული ნამრავლი მეორე გამოსახულების კვადრატისა პირველზე დამატებული მეორე გამოსახულების კუბი.
(a - b)3=a3 - 3a2b + 3ab2 - b3 ორი გამოსახულების სხვაობის კუბი ტოლია პირველი გამოსახულების კუბს გამოკლებული გასამკეცებული ნამრავლი პირველი გამოსახულების კვადრატისა მეორეზე დამატებული გასამკეცებული ნამრავლი მეორე გამოსახულების კვადრატისა პირველზე, გამოკლებული მეორე გამოსახულების კუბი.
4. კუბების ჯამის და სხვაობის ფორმულები:
a3 + b3=(a + b)(a2 - ab + b2) ორი გამოსახულების კუბების სხვაობა ტოლია ამ გამოსახულებების სხვაობის ნამრავლისა მათივე ჯამის არასრულ კვადრატზე.
a3 - b3=(a - b)(a2 + ab + b2) ორი გამოსახულების კუბების ჯამი ტოლია ამ გამოსახულებების ჯამის ნამრავლისა მათივე სხვაობის არასრულ კვადრატზე.ადვილი შესამჩნევია, რომ ფორმულებში a-ს ხარისხები ერთით იკლებს, ხოლო b-ს ხარისხები ერთით იმატებს, ამ თვისების გამო ძნელი არ არის დავწეროთ ორწევრის ნებისმიერი ხარისხი, თუ გვეცოდინება შესაკრებთა კოეფიციენტები. ეს კოეფიციენტები კი შეიძლება შემდეგი ცხრილით გამოვთვალოთ:
ეს არის პასკალის ცხრილი, რომლის რიცხვები შემდეგნაირად მიიღება: ზედა ორის ჯამი იწერება მათ ქვეშ. ორწევრის ნებისმიერი ხარისხის გამოსათვლელად არსებობს ფორმულა რომელსაც ნიუტონის ბინომი ეწოდება და რომელსაც აქვს სახე:
სადაც
n!=1*2*3*...*(n-1)*n
ავტორი: www.edumeter.ge - მამუკა კვინიკაძე
გამოწერა
იყავი ინფორმირებული!
იყავი ინფორმირებული!
ნახეთ ასევე:
კომენტარში უნდა იყოს მინიმუმ 15 სიმბოლო! კომენტარები გაივლის მოდერაციას.
კომენტარი ჯერ არ არის. შენ შეგიძლია იყო პირველი!
