სადაც კი ის შეინიშნება, ყველგან იგრძნობა სილამაზე

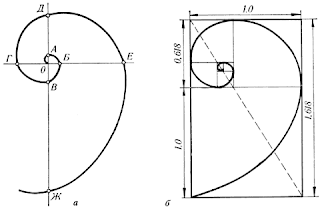
ოქროს კვეთის თეორემა ასე გამოითქმის: ოქროს კვეთა არის მთელის ისეთი გაყოფა ორ, ერთმანეთის არატოლ ნაწილად, როდესაც დიდი ნაწილი ისე შეეფარდება მთელს, როგორც მცირე ნაწილი - დიდს. გეომეტრიაში ოქროს კვეთას საშუალო და კიდურა შეფარდებით გაყოფასაც უწოდებენ. უფრო გასაგები რომ იყოს, განვიხილოთ მონაკვეთი.
A C B
თუ C წერტილი AB მონაკვეთზე ისეა შერჩეული, რომ AC/AB=BC/AC მაშინ ვიტყვით, რომ C წერტილი AB მონაკვეთს ოქროს კვეთის პროპორციით ყოფს. ვთქვათ, AB-ს სიგრძე a ერთეულია, AC=x, მაშინ BC=a-x.
=> x/a=a-x/a პროპორციის ძირითადი თვისებების თანახმად:
x²=a(a-x)
x²=a²-ax
x²+ax-a²=0
მაშასადამე x რიცხვი განტოლების ფესვია.
აქედან x/a=√5-1/2≈0.618.
ოქროს კვეთას ჯერ კიდევ ევკლიდემდე იცნობდნენ. პირველად ეს აღმოაჩინა პითაგორას სკოლის მოსწავლემ ჰიპასოს მეტაფონტელმა. პითაგორას ფილოსოფიურ სკოლაში ფილოსოფიისა მათემატიკის გარდა ჰარმონიასაც სწავლობდნენ. პითაგორელები მონაკვეთის შეფარდებაში მაგიურსა და ზებუნებრივს ეძიებდნენ. ოქროს კვეთა მათთან დიდი პატივით სარგებლობდა. ამ წესის ეს სახელწოდება იმასთან არის დაკავშირებული, რომ სადაც კი იგი შეინიშნება, ყველგან იგრძნობა სილამაზე და ჰარმონიულობა. მაგალითად, ხუროთმოძღვრების ძველ ძეგლებში, სკულპტურულ და ფერწერულ ნაწარმოებებში. შუა საუკუნეებში გაღვივდა ინტერესი ოქროს კვეთისადმი. მას ხშირად იყენებდნენ არა არტო გეომეტრიაში, არამედ ხელოვნებასა და არქიტექტურაში. ამიტომაც, სრულიად ბუნებრივად უნდა მივიჩნიოთ ის ფაქტი, რომ XV საუკუნის დასასრულს დაიწერა სპეციალური წიგნი "ოქროს კვეთის” შესახებ. მის ავტორს, უდიდეს მათემატიკოსს ლუკა პაჩოლის მოჰყავს ოქროს კვეთის ცამეტი თვისება, რომელთაგან თითოეულს ისეთი ეპითეტებით ამკობს, როგრიცაა "განსაკუთრებული”, "უბრწყინვალესი”, "უშესანიშნავესი”, "ენით უთქმელი”, "ზებუნებრივი”, და ასე შემდეგ. განა წიგნის სათაური - "ღვთაებრივი პროპორცია” არ გვჩვენებს ავტორის დამოკიდბულებას ოქროს კვეთისადმი? საინტერესოა, რომ წიგნის დაწერის ერთ-ერთი სულის ჩამდგმელი და მისი გამფორმებელი გენიალური ლეონარდო და ვინჩი იყო. სხვათა შორის, თვით ტერმინი "ოქროს კვეთა” ლეონარდო და ვინჩის მიერაა შემოღებული.
არც კომპოზიტორები და პოეტები დარჩენილან გულგრილნი ოქროს კვეთის მიმართ. მაგალითად, გამოჩენილმა უნგრელმა კომპოზითორმა ბელა ბარტოკმა ბევრი თავისი მუსიკალური ნაწარმოები სწორედ ოქროს კვეთის პრინციპზე დააფუძნა. რას შეეხება პოეტებს, აკადემიკოსი გიორგი წრეთელი აღნიშნავს, რომ პოეზიაში რუსთაველი პირველია მსოფლიოში - და შეიძლება ერთადერთი, რომელმაც ოქროს კვეთის პრინციპზე ააგო ესოდენ დიდი მოცულობის პოეტური მაწარმოები. მისი პოემის 1662 სტროფიდან 863 ოქროს კვეთის პრინციპზეა აგებული.
დაკვირვება ცხადყოფს, რომ ესთეტიკური თვალსაზრისით ოქროს კვეთას გარკვეული უპირატესობა აქვს. ამის დამადასტურებელია იმ ცდის შედეგები, რომელიც გასული საუკუნის ბოლოს ჩაატარეს. გამოსაცდელ პირს ათ სხვადასხვა მართკუთხედს სთავაზობდნენ. რომელთაგან მას ერთი უნდა აერჩია. მართკუთხედებს შორის იყო "ოქროს მართკუთხედიც” გვერდების შეფარდებით 21:34. გამოსაცდელთა 22%-მა სწორედ ეს მართკუთხედი აირჩია. აგრეთვე საფოსტო ბარათებს, საფულეებს, შოკოლადის ფილებს და ბევრ სხვა საგანს ოქროს მართკუთხედის ფორმა აქვს. ოქროს კვეთის პროპორციის კიდევ ერთი თვალსაჩინო მაგალითია ფიბონაჩის რიცხვები. განვიხილოთ რიცხვთა (Un) მიმდევრობა, რომლის პირველი ორი წევრი უდრის 1-ს, ხოლო ყოველი შემდგომი წინა ორი წევრის ჯამს.
ამრიგად U1=1; U2=1; Un+2=Un+1+Un.
(n=123
123…..) ეს მიმდევრობა ფიბონაჩის მიმდევრობის სახელითაა ცნობილი. შემოიღო XII – XIII საუკუნეების გამოჩენილმა იტალიელმა მათემატიკოსმა ლეონარდო პიზელმა, რომელსაც მეტსახელად ფიბონაჩი ერქვა. (ფიბონაჩი იყო ფიბონაჩის ვაჟიშვილი). აი ამ მიმდევრობის რამდენიმე საწყისი წევრი:
1; 1; 2; 3; 5; 8; 13; 21; 34; 55; 89…
ფიბონაჩის მიმდევრობის ნებისმიერი წევრის მომდევნო წევრთან შეფარდება არის ოქროს კვეთის შეფარდების მიახლოვებითი მნიშვნელობა.
ოქროს კვეთით კარგად გამოიყოფა, მაგ: ….3; 5; 8; 13; 21…. და მათი გაყოფის შედეგად მიღებული ნაწილებისაგან შედგენილი წილადები იძლევიან კარგ მიახლოვებას:
3/5≈5/8≈8/13≈13/21….
 ასეთი სილამაზის შემხედვარე ვერც ერთი არქიტექტორი და ხელოვანი ვერ დარჩებოდა გულგრილი ოქროს კვეთის მიმართ. ამიტომ, ოქროს კვეთას იყენებდნენ ხუროთმოძღვრებასა და ხელოვნებაში. ხელოვნებადმცოდნეებმა აზროვნების შედეგად დაადგინეს, რომ ბევრ ხუროთმოძღვრულ შედევრში სწორედ ოქროს კვეთის პროპორციაა გამოყენებული. აქ გვერდს ვერ ავუვლით ჩვენი სახელოვანი მხატვრის სერგო ქობულაძის ჯერაც გამოუქვეყნებელ გამოკვლევას, სადაც დასაბუთებულია, რომ მცხეთის ჯვრის დიდებული ტაძარი სწორედ ოქროს კვეთის პროპორციის მიხედვით არის აგებული. ქრისტიანული რელიგიის გამოცხადების შემდგეგ, მეფე მირიანის დროს აღიმართა ხის დიდი ჯვარი, რომელიც განკუთვნილი იყო მის დასავლეთით აღმართული არმაზის კერპის დასათრგუნავად. მირიანის შვილმა რევიმ კი ამ ჯვრის გარშემო გადახურული ნაგებობა ააგო, რათა ეს ჯვარი უფრო დაცული ყოფილიყო. ტაძარი აშენდა VI საუკუნეში - გუარამის მემკვიდრის, სტეფანოზის მიერ. ჯვარი კი მის ცენტრში მოხვდა. სამხრეთის კარის თავზე ჯვრის ამაღლების კომპოზიციაა, აღმოსავლეთის ფასადზე კი დემეტრეს, სტეფანოზისა და ადარნესეს გამოსახულებებია.
ასეთი სილამაზის შემხედვარე ვერც ერთი არქიტექტორი და ხელოვანი ვერ დარჩებოდა გულგრილი ოქროს კვეთის მიმართ. ამიტომ, ოქროს კვეთას იყენებდნენ ხუროთმოძღვრებასა და ხელოვნებაში. ხელოვნებადმცოდნეებმა აზროვნების შედეგად დაადგინეს, რომ ბევრ ხუროთმოძღვრულ შედევრში სწორედ ოქროს კვეთის პროპორციაა გამოყენებული. აქ გვერდს ვერ ავუვლით ჩვენი სახელოვანი მხატვრის სერგო ქობულაძის ჯერაც გამოუქვეყნებელ გამოკვლევას, სადაც დასაბუთებულია, რომ მცხეთის ჯვრის დიდებული ტაძარი სწორედ ოქროს კვეთის პროპორციის მიხედვით არის აგებული. ქრისტიანული რელიგიის გამოცხადების შემდგეგ, მეფე მირიანის დროს აღიმართა ხის დიდი ჯვარი, რომელიც განკუთვნილი იყო მის დასავლეთით აღმართული არმაზის კერპის დასათრგუნავად. მირიანის შვილმა რევიმ კი ამ ჯვრის გარშემო გადახურული ნაგებობა ააგო, რათა ეს ჯვარი უფრო დაცული ყოფილიყო. ტაძარი აშენდა VI საუკუნეში - გუარამის მემკვიდრის, სტეფანოზის მიერ. ჯვარი კი მის ცენტრში მოხვდა. სამხრეთის კარის თავზე ჯვრის ამაღლების კომპოზიციაა, აღმოსავლეთის ფასადზე კი დემეტრეს, სტეფანოზისა და ადარნესეს გამოსახულებებია.
 ოქროს კვეთითაა აგებული ანტიკური საბერძნეთის ბევრი არქიტექტურული ძეგლი - მაგ: ათენის პანთეონი (ძვ.წ. V ს.). აღნიშნული ძეგლის სიმაღლის შეფარდება მის სიგრძესთან 0.618-ის ტოლია. ასევე ოქროს კვეთის პრინციპზეა დახატული ტიციანის, ლეონარდო და ვინჩის, რაფაელის სურათები და დიუერის ავტროპორტრეტი. მათე თევდორეს ძე კაზაკოვის მიერ შექმნილი არქიტექტურული ძეგლები ანალიზი გვიჩვენებს, რომ ის ფართოდ იყენებდა "ოქროს კვეთას”. მან ოქროს კვეთის გამოყენებით ააგო მრავალი შენობა. კერძოდ, "პეტრეს სასახლე მოსკოვში” (ახლა ჟუკოვსკის სახელობის სამხედრო საჰაერო აკადემია), მოსკოვის სათავადაზნაურო საკრებულო. (ამჟამად კავშირების სახლი) და მოსკოვის უნივერსიტეტის ძველი შენობა. ე.ი: არქიტექტურა არის გეომეტრიულ აზროვნებაში წარმოდგენილი ყვავილები, რომლებიც მდუმარებაში იძლევიან მუსიკის შეგრძნებას. არქიტექტურა ერთგვარი მატეანეა მსოფლიოსი, სადაც თავისთავად შეიძლება მოვიპოვოთ იმ დროის მკაცრი თუ ლირიკული პერსონაჟები. ქანდაკებაში და არქიტექტურაში ხუროთმოძღვარი უნდა ჰგავდეს უფრო პოეტს, ვიდრე სარდალს ან ბრძენს.
ოქროს კვეთითაა აგებული ანტიკური საბერძნეთის ბევრი არქიტექტურული ძეგლი - მაგ: ათენის პანთეონი (ძვ.წ. V ს.). აღნიშნული ძეგლის სიმაღლის შეფარდება მის სიგრძესთან 0.618-ის ტოლია. ასევე ოქროს კვეთის პრინციპზეა დახატული ტიციანის, ლეონარდო და ვინჩის, რაფაელის სურათები და დიუერის ავტროპორტრეტი. მათე თევდორეს ძე კაზაკოვის მიერ შექმნილი არქიტექტურული ძეგლები ანალიზი გვიჩვენებს, რომ ის ფართოდ იყენებდა "ოქროს კვეთას”. მან ოქროს კვეთის გამოყენებით ააგო მრავალი შენობა. კერძოდ, "პეტრეს სასახლე მოსკოვში” (ახლა ჟუკოვსკის სახელობის სამხედრო საჰაერო აკადემია), მოსკოვის სათავადაზნაურო საკრებულო. (ამჟამად კავშირების სახლი) და მოსკოვის უნივერსიტეტის ძველი შენობა. ე.ი: არქიტექტურა არის გეომეტრიულ აზროვნებაში წარმოდგენილი ყვავილები, რომლებიც მდუმარებაში იძლევიან მუსიკის შეგრძნებას. არქიტექტურა ერთგვარი მატეანეა მსოფლიოსი, სადაც თავისთავად შეიძლება მოვიპოვოთ იმ დროის მკაცრი თუ ლირიკული პერსონაჟები. ქანდაკებაში და არქიტექტურაში ხუროთმოძღვარი უნდა ჰგავდეს უფრო პოეტს, ვიდრე სარდალს ან ბრძენს.
მათი საშუალო არითმეტიკული b=a+c/2, ხოლო საშუალო გეომეტრიულია b=√ac და საშუალო ჰარმონიულია b=2ac/a+c. ორი რიცხვის საშუალო ჰარმონიულის პოვნას ჰარმონიული გაყოფა ეწოდება. საშუალო ჰარმონიული გამოიყენება მუსიკის თეორიაში. ცნობილია, რომ მუსიკის თეორიაში ტონის სიმაღლე განისაზღვრება დროის ერთეულში რხევათა რიცხვით, ორი ტონის ინტერვალი კი რხევათა რიცხვის შეფარდებით. დავუშვათ, რომ do, ტონი დროის ერთ ერთეულში განისაზღვრება რაღაც რხევათა რიცხვით, იმავე რხევათა რიცხვს ერთი ოქტავით მაღალი ტონი აქვს დროის ½ ერთეულში, მათი საშუალო ჰარმონიული კი 1 და ½ -ს შორის იქნება 2∙1∙½ / 1+ ½=2/3 ეს რიცხვი ახასიათებს ინტერვალ კვანტას do1 დან SOE - მდე. საშუალო ჰარმონიული do1 -სა და SOE - ს შორის. ე.ი.: 1 - სა და 2/3 რიცხვებს შორის.
2∙1∙2/3 / 1+2/3 =4/5 ამის შესაბამის ინტერვალს ეწოდება დიდი ტერცია do-დან, ხოლო მისი ზედა ტონია m. ასე წარმოიქმნება გამა რიცხვი. მაგრამ, ვამბობთ მუსიკა, მუსიკა… ბოლოს და ბოლოს რა არის მუსიკა? სიტყვა მუსიკა ძველმა ბერძნებმა გვაჩუქეს. იგი წარმოიშვა "მუზადან”. მუზები ძველ ბერძნულ მითოლოგიაში იყვნენ ღმერთების მეფის, ზევსის ქალიშვილები. ისინი მფარველობდნენ ხელოვნებისა და მეცნიერების დარგებს. მუზა სულ ცხრა იყო. თუმცა, ამ ცხრა დას შორის კონკრეტულად არცერთი არ მფარველობდა მუსიკას. და მაინც რა არის მუსიკა? ეს არის გრძნობები და განცდები, გადმოცემული ბგერებით. მუსიკა გვეხმარება შევიგრძნოთ იმდენად მნიშვნელოვანი რამ, იმდენად მნიშვნელოვანი, რომ სიტყვითაც კი ვერ გადმოვცემთ. ჭკვიანმა გერმანელმა პოეტმა ჰაინრიხ ჰაენემ ამის შესახებ თქვა: "მუსიკა იწყება იქ, სადაც მთავრდება სიტყვა”. ე.ი: მუსიკით შეიძლება გადმოიცეს ისიც კი რასაც სიტყვებით ვერ გადმოსცემ. მაგრამ, ზოგჯერ სიტყვა ისეთ სილამაზეს ქმნის, რომ მასთან ყოველგვარი სილამაზე ითრგუნება
 რადგან სიტყვის სიალმაზეს შევეხეთ, არ შეიძლება გვერდი ავუაროთ შოთა რუსთაველის "ვეფხისტყაოსნის” ფენომენს. 1973 წელს გამომცემლობა "მეცნიერებამ” გამოაქყვეყნა აკადემიკოს გიორგი წრეთლის მონოგრაფია "მეტრი და რითმა ვეფხისტყაოსანში”. აკად. გ. წრეთლი ასაბუთებს, რომ რუსთაველის გენიალური ქმნილება სიმეტრიასა და ოქროს კვეთაზეა აგებული. დღემდე შეუმჩნეველი დარჩა რომ "ვეფხისტყაოსნის” სიმფონია ძირითადად "ოქროს კვეთას” ემყარება. "ვეფხისტყაოსანში” ოქროს კვეთის, ანუ ღვთაებრივი პროპორციის გამოვლენა ახლებურად სვამს საკითხს რუსთაველის ლექსის მეტრიკული სტრუქტურის შესახებ, ხოლო მის ავტორს სრულებით განსაკუთრებულ ადგილს ანიჭებს მსოფლიო პოეზიის ისტორიაში. ვიცით, რომ შაირით არის დაწერილი შ. რუსთაველი გენიალური ქმნილება - "ვეფხისტყაოსანი”. ქართულ ლექსში ორი სახის შაირი გვხვდება: მაღალი და დაბალი. მათი სხვადასხვაობა გამოწვეული შემდეგი გარემოებით. შაირით დაწერილი ტაეპები ორგვარი აღნაგობისაა - ერთი სახის შაირის ტაეპები იკითხება ჩქარი ტემპით, რადგან იგი ოთხმარცვლიანი ტერფისაგან შედგება. (მარცვალთა ჯგუფს, როელიც შედგება ერთი მახვილი და რამდნეიმე უმახვილო მარცვლისაგან, ტერფი ეწოდება. ტერფი უმარტივესი რიტმული ერთეულია).
რადგან სიტყვის სიალმაზეს შევეხეთ, არ შეიძლება გვერდი ავუაროთ შოთა რუსთაველის "ვეფხისტყაოსნის” ფენომენს. 1973 წელს გამომცემლობა "მეცნიერებამ” გამოაქყვეყნა აკადემიკოს გიორგი წრეთლის მონოგრაფია "მეტრი და რითმა ვეფხისტყაოსანში”. აკად. გ. წრეთლი ასაბუთებს, რომ რუსთაველის გენიალური ქმნილება სიმეტრიასა და ოქროს კვეთაზეა აგებული. დღემდე შეუმჩნეველი დარჩა რომ "ვეფხისტყაოსნის” სიმფონია ძირითადად "ოქროს კვეთას” ემყარება. "ვეფხისტყაოსანში” ოქროს კვეთის, ანუ ღვთაებრივი პროპორციის გამოვლენა ახლებურად სვამს საკითხს რუსთაველის ლექსის მეტრიკული სტრუქტურის შესახებ, ხოლო მის ავტორს სრულებით განსაკუთრებულ ადგილს ანიჭებს მსოფლიო პოეზიის ისტორიაში. ვიცით, რომ შაირით არის დაწერილი შ. რუსთაველი გენიალური ქმნილება - "ვეფხისტყაოსანი”. ქართულ ლექსში ორი სახის შაირი გვხვდება: მაღალი და დაბალი. მათი სხვადასხვაობა გამოწვეული შემდეგი გარემოებით. შაირით დაწერილი ტაეპები ორგვარი აღნაგობისაა - ერთი სახის შაირის ტაეპები იკითხება ჩქარი ტემპით, რადგან იგი ოთხმარცვლიანი ტერფისაგან შედგება. (მარცვალთა ჯგუფს, როელიც შედგება ერთი მახვილი და რამდნეიმე უმახვილო მარცვლისაგან, ტერფი ეწოდება. ტერფი უმარტივესი რიტმული ერთეულია).
შავი ცხენი/ სადავითა/ ჰყვა ლომსა და/ ვითა გმირსა/
მეორე სახის შაირი ასეთი ტერფისაგან შედგება.
2 3 3 2 3 3
იყო/ არაბეთს/ როსტევან/ მეფე/ ღმრთისაგან/ სვიანი/.
ეს ტერფი ექვსტერფიანია. ამის გამო ის ნელი ტემპით იკითხება. რიტმულად ჩქარი ტემპის მქონე ტერფებისაგან შედგენილ შაირს მაღალი შაირი ეწოდება, ხოლო რიტმულად ნელი ტემპის მქონე ტერფებისაგან შედგენილ შაირს - დაბალი შაირი.
ვეფხისტყაოსნის 1662 სტროფიდან 863 ოქროს კვეთის პრინციპზეა აგებული. მაგ:
3 5 3 5
რა ჭირი/ კაცსა სოფელმან/ მოუთმლის/ მოუთმინამან/
8 8
3 5 3 5
სარიდან/ ერქვა სახელად/ მტერთა სვრად/ დაუფარავი/
8 8
როგორც ვხედავთ, მივიღეთ შეფარდება 3:5:8. ეს კი არის ოქროს კვეთის შეფარდება 3:5≈0.6. 5:8≈0.6.
გ. წერეთელი აღნიშნავდა, რომ შოთა რუსთაველის მიერ "ოქროს კვეთის” შეფარდების პროპორციის გამოყენება "ვეფხისტყაოსანში” არ იყი შემთხვევითი ე.ი.: რუსთაველმა პოეზიაში მოგვცა სრულყოფილი სიმეტრია, მსგავსად იმისა, როგორც ტიციანმა, რაფაელმა, ლეონარდი და ვინჩიმ მხატვრობასა და ხელოვნებაში და ახლა, როდესაც ეს სრულყოფილება გამოვლენილია, ქართველი პოეტის ადგილი მსოფიო პოეზიის ისტორიაში სრულდებით განსაკუთრებულად გვესახება. ეს უდიდესი სილამაზეა, მაგრამ რა არის სილამაზე? სილამაზე ბუნების სიბრძნეა. სილამაზე არის იმედის შუქთა ციმციმი. კარგი თავლების გამომეტყველების გარეშე, თვით ყველაზე ლამაზი ნაკვთებიც კი უფერული ხდება. გარეგნული სილამაზე არასდროს იქნება სრულყოფილი, თუ იგი შინაგანი მშვენიერებით არ იქნება გასხივოსნებული. "ოქროს კევთის” პროპორციამ უდიდესი პოპულარობა მოიპოვა იტალიაში. შუა საუკუნეებში, აღორძინების პერიოდში ოქროს კვეთას იყენებდნენ არა მარტო გეომეტრიაში, არამედ ხელოვნების სხვადასხვა დარგში. ოქროს კვეთის პროპორცია ჩანს ადამიანის სხეული აგებულენაშიც. ადამიანი ლამაზია, თუ სახის ნაკვთები ისეთი პროპორციით აქვ განლაგებული, რომლის შეფარდება 0,618.
 ოქროს კევთის მაგალითია აპოლონის ქანდაკება. მისი ძირითადი ნაწილები დაყოფილია ოქროს კვეთის მიხედვით. აპოლონ ბელვედელის ქანდაკება შესრულებულია ბრძენი მოქანდაკის - ლეოქარის მიერ ჩვ. წ. აღ-მდე IV საუკუნეში. აგრეთვე ადამიანის სხეული ითვლება ლამაზად, თუ შესრულებულია პროპორცია: თავი ისე უდნა შეეფარდებოდეს ტანს როგორც თანი მთლიანი სხეულის სიგრძეს. A:b=b:c
ოქროს კევთის მაგალითია აპოლონის ქანდაკება. მისი ძირითადი ნაწილები დაყოფილია ოქროს კვეთის მიხედვით. აპოლონ ბელვედელის ქანდაკება შესრულებულია ბრძენი მოქანდაკის - ლეოქარის მიერ ჩვ. წ. აღ-მდე IV საუკუნეში. აგრეთვე ადამიანის სხეული ითვლება ლამაზად, თუ შესრულებულია პროპორცია: თავი ისე უდნა შეეფარდებოდეს ტანს როგორც თანი მთლიანი სხეულის სიგრძეს. A:b=b:c
იყავი ინფორმირებული!